Ingat trigonometri? Atau mungkin kamu lagi mempelajarinya sekarang? Pernah merasa kalau trigonometri itu susah?
Kamu nggak sendiri.
Banyak orang yang bahkan setelah terjun di dunia teknik masih merasa aneh dengan bidang matematika ini.
Mungkin kamu sudah tahu, salah satu penyebabnya adalah karena angka-angka yang terlibat dalam sin cos tan itu ga bisa ditambah kurang kali bagi dengan gampang. Misalnya:
-
(\sin(2) + \sin(3)) itu ga sama dengan (\sin(5)),
-
(\sin(2) \times \sin(3)) itu ga sama dengan (\sin(6)).
Ini bikin otak kita kayang dan koprol. Soalnya beda banget sama aritmatika yang biasanya kita kenal sejak kecil.
Karena ga intuitif akhirnya kita harus hafalkan beberapa rumus untuk mengingat sifat-sifat fungsi-fungsi ini dan supaya bisa mengolah angka-angka untuk mendapatkan jawaban yang kita inginkan.
Ga cuma itu, coba lihat tabel nilai sin cos tan untuk di bawah ini. Untuk sudut-sudut yang katanya "sederhana" seperti ini saja, angka-angkanya aneh dan ada akarnya.
|[\theta] | [30^\circ] | [45^\circ] | [45^\circ]
|[\sin\theta]| [\frac{1}{2}]| [\frac{\sqrt{2}}{2}]| [\frac{\sqrt{3}}{2}]
|[\cos\theta]| [\frac{3}{2}]| [\frac{\sqrt{2}}{2}]| [\frac{1}{2}]
|[\tan\theta]| [\frac{3}{3}]| [1] | [\sqrt{3}]
Udah gitu gampang ketuker mana yang akar 3 mana yang akar 2. Dan memang, sebenarnya ini misteri yang sangat dalam. Cos itu apa sih? Sin itu apa sih?
Ga jelas.
Aku kasih tahu sebuah rahasia nih. Sebenarnya sin cos tan dan keluarganya itu pada dasarnya angkanya harus dihafal. Ga bisa dihitung.
Saat trigonometri lahir, orang jaman dulu nggak bisa ngitung kalau sudut sekian itu cos nya berapa. Mereka harus lihat tabel seperti di atas.
Semua yang kita tahu soal nilai angka sin cos tan itu cuma hasil dari kita mengamati ukuran segitiga, lalu dicatat dan diingat dalam bentuk tabel.
Serius.
Baru setelah perkembangan matematika melejit sekitar abad 16-17 Masehi baru kita mulai paham wujud asli trigonometri.
Sepanjang SMA saya juga selalu merasa trigonometri membingungkan. Tapi karena perlu untuk ujian masuk kuliah, saya bertahan dalam ketidakpahaman. Baru setelah di tahun kedua/ketiga kuliah ada sedikit pencerahan tentang polemik trigonometri ini. Pemecahannya ternyata perlu imajinasi yang kuat.
Semua Terjawab Dalam Imajinasi
Penyebab tingkah laku aneh dari angka dalam trigonometri itu adalah karena kita sibuk mengejar "bayangan" dari angka-angka itu.
Bayangan?
Iya.
Yang kita berusaha hitung dalam trigonometri hanyalah bayangan dari monster yang sebenarnya.
Wujud asli dari monster trigonometri ini akan tampak jelas kalau kita masuk ke dimensi tempat dia tinggal: Alam Khayalan.
Yah, lebih tepatnya sih alam kompleks sih ya. Maafin lah, demi impact. (Buat yang pengen baca lebih banyak soal alam kompleks bisa dibaca di Wikipedia).
Buat yang sudah tahu tentang bilangan kompleks dan imajiner santai lah ya, kalian pasti tahu yang aku omongin 1). Singkat cerita, alam kompleks adalah dimensi tersembunyi yang ada di balik garis bilangan nyata. Di mana perubahan-perubahan yang terjadi di dalamnya cuma bisa mempengaruhi dunia nyata secara tidak langsung, seperti bayangan.
Wujud Asli Monster Trigonometri
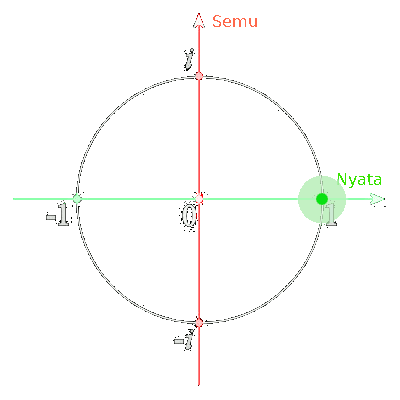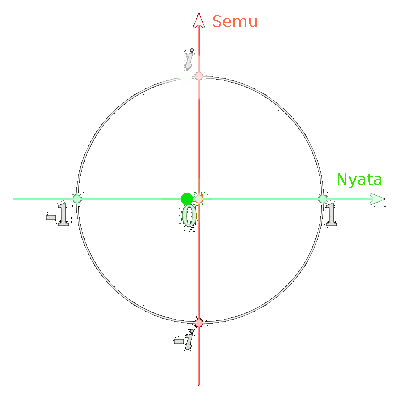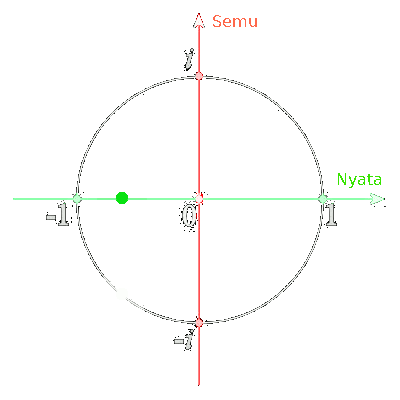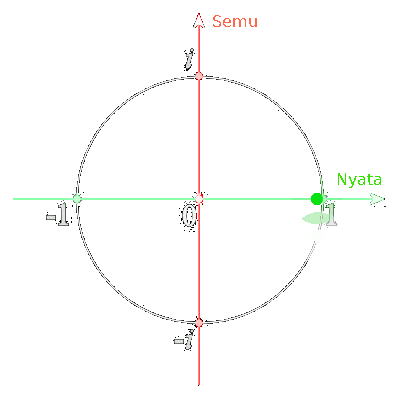
Wujud asli dari monster trigonometri adalah titik dalam lingkaran. Lingkaran yang mengitari angka nol dalam garis bilangan. Biasanya jari-jarinya 1, seperti gambar di bawah ini.
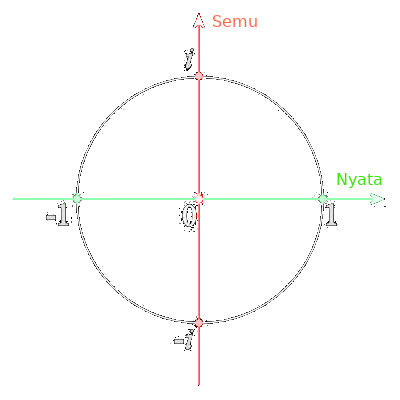
Kita manusia, sebagai makhluk nyata, tak bisa melihat lingkaran ini. Yang bisa kita lihat hanyalah garis hijau antara titik 1 dan -1. Bayangkan melihat sebuah CD persis dari samping, dia akan kelihatan seperti garis lurus. Inilah yang kita lihat sebagai bayangan dari trigonometri.
Saat kita melihat angka-angka sin-cos-tan itu bergerak-gerak bolak-balik antara 1 dan -1, kita lihat dia bergerak dalam garis lurus. Padahal sebenarnya di alam habitat aslinya, dia sedang berputar-putar dalam sebuah lingkaran. Gerakannya seperti di bawah ini.
Jaman abad 16-17 itu penelitian tentang alam khayal ini mulai gencar, dan orang-orang mulai paham bagaimana caranya berhitung dalam alam khayal. Di saat itulah, ada orang jenius namanya Euler yang berhasil menemukan cara menghitung pergerakan memutar ini dengan rapih.
Dia menemukan kalau gerakan memutar yang bolak-balik secara sempurna ini adalah hasil dari perpangkatan dari angka [e (dua koma tujuh sekian-sekian aku ga hafal wkwkkw)](https://en.wikipedia.org/wiki/E_(mathematical_constant) terhadap angka sudut yang dikalikan dengan i (satuan semu).
Apa itu satuan semu? Satuan semu adalah angka yang kalau dikuadratkan (dikalikan dengan dirinya sendiri) akan jadi -1.
Kenapa perpangkatan bisa jadi perputaran?
Ini adalah salah satu sifat unik alam khayalan tersebut. Sedikit banyak ada hubungannya sama perkalian dengan bilangan semu yang mengasilkan perputaran. Perhatikan proses berikut sambil lihat gambar di atas tadi:
- 1 dikalikan dengan i jadi i (sebelah atas)
- i dikalikan dengan i jadi -1 (sebelah kiri)
- -1 dikalikan dengan i jadi -i (sebelah bawah)
- -i dikalikan dengan i jadi 1 (kembali ke kanan lagi)
Tuh, padahal cuma hanya mengalikan dengan i saja, angkanya jadi berputar-putar.
Kalau mau memahami ini lebih lanjut silahkan pelajari bilangan kompleks, benar-benar alam matematika yang misterius dan unik.
Perpangkatan Jauh Lebih Sederhana Daripada Trigonometri
Perpangkatan itu operasi matematika yang lumayan sederhana. Paling nggak lebih sederhana dari sin ataupun cos. Kita tahu cara ngitung pangkat. Dan kita ga perlu liat tabel hasil catatan pengamatan yang dibikin orang untuk tahu hasilnya.
Karena penemuan Euler inilah sekarang kita bisa menghitung 2) sin cos tan, dalam arti sebenarnya. Benar-benar menghitung. Bukan lihat kejadian di alam, terus dicatat dalam tabel. Dan bukan hanya sekedar menghitung, tapi juga memahami esensinya yang lebih dalam.
Catatan kaki:
1) Teman-teman yang lebih tahu dari saya juga mungkin bertanya-tanya, kenapa langsung lompat ke bilangan kompleks tanpa menjelaskan konsep-konsep yang lebih sederhana. Yah, saya bukan mau ngajarin trigonometri, tapi cuma mau cerita soal kaitannya dengan bilangan kompleks aja.
2 ) Untuk menghitung ini secara praktis, sebenarnya ada alat lain yang tak kalah pentingnya, yaitu pengembangan deret. Tapi simpan dulu buat lain waktu.